Bu yazımızda NURBS (Non-Uniform Rational B Spline ) sınıflarını
inceleyeceğiz ve az sayıda koordinatlarla eğrinin/yüzeyin nasıl gösterilebileceğini
inceleyeceğiz.
Matematiksel temelleri :
Grafiksel programlarda her zaman elimizde denklemi olan
yüzeyler olmaz, dolayısı ile koordinatlarını bildiğimiz bir sistemi nasıl gösterebiliriz?
Diyelim elimizde üç nokta var ve grafiğimiz sadece bu üç noktadan oluşuyor. Bu
üç noktadan bir çizgi mi geçecek? Yoksa bir parabol mu yoksa tamamen başka bir
fonksiyon mu? Bunların cevabı çoğu zaman kullanıcıya kalmıştır. Kısaca söylemek gerekirse
tanımlayacağımız parametreler ışığında elimizdeki noktalara uygun bir fonksiyon tanımlanacak
ve o fonksiyonun görüntüsü alınacak.İşin uyguluma kısmından önce NURBS nedir
kısaca açıklayayım. Uniform veya Non Uniform kontrol noktalarının eğri üzerindeki
etkisini belirlemektedir.Örneğimizde Non-Uniform bir spline kullanılmıştır.Uniform
spline kullanmak isteseydik bütün değerleri artarak giden değerler olarak girecektik.B-Spline
ise özel bir fonksiyondur.Bu fonksiyon ile noktalarımız en optimum eğri denklemini
verecektir.Ayrıca değişik Spline fonksiyonları da vardır (cubic,quadratic,TPS,RBF,MQ...).Nümerik
metod dersi almış olanlar kaynaklarından bakarak bu fonksiyonlara erişebilirler.
Yeni Sınıflarımız :
|
Sınıf |
Açıklama |
|
SoNurbsCurve : |
Eğrinin bilgilerinin ve metodlarının tutulduğu sınıf.
Bu sınıf bizden knot vektörlerini ve koordinatları beklemektedir. Knot vektörleri
eğrinin şeklini belirleyecektir. Elimizdeki nokta sayısına ek olarak 8 tane fazla
knot tanımlayabiliriz. Bu bize maksimum 8. dereceden bir eğri verecektir. Yani elimizde
10 tane nokta varsa knot sayısı 18 olacaktır. Detaylı örneği kod üzerinde açıklayacağım. |
|
SoCoordinate3
: |
3 Boyutlu koordinatların
ve metodlarının tutulduğu sınıftır. Amacı görüntü üretmek değil koordinat bilgileri
değişik sınıfların kullanabileceği şekilde saklamaktır. |
|
SoDrawStyle
: |
Renderin nasıl
edileceğini belirlememizi sağlayan sınıftır. Render işleminin çizgisel mi noktasal
mı olacağını ve bunun özelliklerini belirler. |
Uygulama
:
Uygulama olarak
heliks tarzında, z yönünde arttıkça çapı küçülen 13 nokta tanımlıyoruz.Daha sonra
bu noktalara uyacak şekilde bir eğri tanımlıyoruz, bunun için ise knotları tanımlıyoruz.
Kodda da görebileceğiniz gibi 17 knot tanımladık ve değerlere dikkat ederseniz bu
knotlar ya sabit kalmakta ya da artmaktadır. Örnek üzerinde bu değerlerin ağırlıklarını
açıklayacağım.
Uygulama Kodumuz
:
// yeni headerler ekliyoruz bunlar SoDrawStyle,SoCoordinate3 ve SoNurbsCurve
// bu koda yeni bakıyorsanız bir önceki yazımı okumanızı tavsiye ederim
#include <Inventor/Qt/SoQt.h>
#include <Inventor/Qt/SoQtRenderArea.h>
#include <Inventor/Qt/viewers/SoQtExaminerViewer.h>
#include <Inventor/SoDB.h>
#include <Inventor/nodes/SoCone.h>
#include <Inventor/nodes/SoCube.h>
#include <Inventor/nodes/SoDirectionalLight.h>
#include <Inventor/nodes/SoGroup.h>
#include <Inventor/nodes/SoMaterial.h>
#include <Inventor/nodes/SoPerspectiveCamera.h>
#include <Inventor/nodes/SoRotation.h>
#include <Inventor/nodes/SoSeparator.h>
#include <Inventor/nodes/SoSphere.h>
#include <Inventor/nodes/SoTranslation.h>
#include <Inventor/sensors/SoTimerSensor.h>
#include <Inventor/actions/SoGLRenderAction.h>
#include <qapplication.h>
#include <qgroupbox.h>
#include <qlayout.h>
#include <Inventor/nodes/SoEventCallback.h>
#include <Inventor/events/SoKeyboardEvent.h>
#include <Inventor/sensors/SoTimerSensor.h>
#include <Inventor/actions/SoGLRenderAction.h>
#include <Inventor/nodes/SoDrawStyle.h>
#include <Inventor/nodes/SoComplexity.h>
#include <Inventor/nodes/SoCoordinate3.h>
#include <Inventor/nodes/SoNurbsCurve.h>
// global olarak controlPts nesnesini tanımlıyoruz
SoCoordinate3 *controlPts;
// Şeklimizin koordinatlarını aşağıda tanımlıyoruz
float pts[13][3] = {
{ 6.0, 0.0, 6.0},
{-5.5, 0.5, 5.5},
{-5.0, 1.0, -5.0},
{ 4.5, 1.5, -4.5},
{ 4.0, 2.0, 4.0},
{-3.5, 2.5, 3.5},
{-3.0, 3.0, -3.0},
{ 2.5, 3.5, -2.5},
{ 2.0, 4.0, 2.0},
{-1.5, 4.5, 1.5},
{-1.0, 5.0, -1.0},
{ 0.5, 5.5, -0.5},
{ 0.0, 6.0, 0.0}};
/* Eğrimizin şeklini belirleyen asıl kısım aşağıda bu değerler ile eğrimizin hangi
noktada ne kadar eğik olacağı belirlenmektedir */
float knots[17] = {0, 0, 0, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 10, 10, 10};
void main(int argc, char **argv)
{
QWidget *myWindow = SoQt::init(argv[0]);
if (myWindow == NULL) exit(1);
// Ana nesnemizi oluşturuyoruz
SoSeparator *curveSep = new SoSeparator;
curveSep->ref();
// SoDrawStyle nesnesi oluşturup bunun genişliğini 4 yapıyoruz
SoDrawStyle *drawStyle = new SoDrawStyle;
drawStyle->lineWidth = 4;
curveSep->addChild(drawStyle);
// Yeni bir koordinat nesnesi ve NurbsCurve nesnesi oluşturuyoruz
controlPts = new SoCoordinate3;
SoNurbsCurve *curve = new SoNurbsCurve;
/* Aşağıda gördüğünüz gibi SoCoordinate3 nesnesinin setValues metodu
bizden başlangıç noktasını ve kaç tane nokta vermemiz gerektiğini ve noktaları ister
*/
controlPts->point.setValues(0, 13, pts);
/* kontrol noktalarını 13 olarak ayarlıyoruz bu örneğimizde kontrol
nokta sayısı koordinat sayısı ile eşit */
curve->numControlPoints = 13;
/* En son olarak knot vektörünün değerlerini nesnemize geçiriyoruz
*/
curve->knotVector.setValues(0, 17, knots);
/* addChild metodları ile nesneleri birbirlerine ekliyoruz */
curveSep->addChild(controlPts);
curveSep->addChild(curve);
SoQtExaminerViewer *myViewer = new SoQtExaminerViewer(myWindow);
myViewer->setSceneGraph(curveSep);
SoQt::show(myWindow);
SoQt::mainLoop();
//return 0;
}
|
Kodu çalıştırınca :
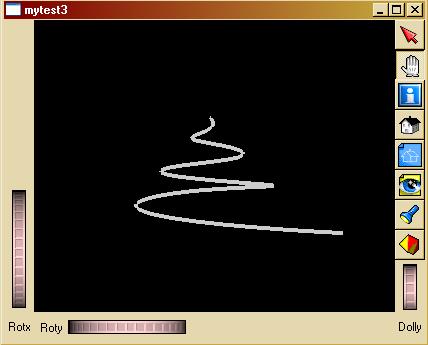
Gelelim knot vektörü içinde ki değerlerin anlamlarına
: knot vektörü içindeki değerler kontrol noktalarında "basis functionun" başlayacağını
ve biteceğini belirtmektedir. Sizin bilmeniz gereken tek şey şu; hangi noktalarda
tekrar varsa o koordinattaki değerler eğrinin şeklini daha fazla belirlemektedir.
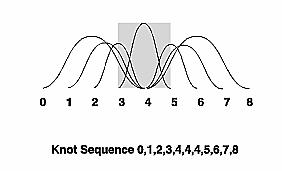 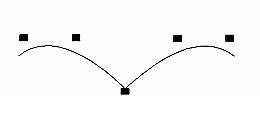 (1) (1)
Yukarıda gördüğünüz örnekte, sağ tarafta elimizde
5 tane koordinat var (siyah noktalar) ve buna bir eğri tanımlıyoruz. Solda ise knot
diyebileceğimiz dizi var. Knottaki değerlerin herbiri o noktadaki koordinatın etkisinin
vermektedir. Dolayısı ile ortalarda 4,4,4 olması bize orta noktadaki değerin
fazla ağırlığı olduğunu göstermektedir. Eğer eğrimizin başlangıç ve bitiş noktalarından
geçmesini istiyorsak yukarıdaki diziyi 0,0,0,1,2,3,4,4,4 yaparsak eğrimiz başlangıç
ve bitiş noktalarından geçer ve eğri orta noktada daha düz bir eğim alır.
Sonuç olarak :
Genelde cisimlerin denklemleri olmadığı için(küre,küp,koni
gibi) mecburen koordinatlardan yola çıkarak cismin şeklini kestirmeye çalışırız. Bunu
yaparken de değişik fonksiyonlarla bu noktalardan anlamlı şekil çıkartırız. Fonksiyonları
tanımlamak için de knot vektörlerini kullanırız. NURBS sınıfları işte bu noktada kullanılmaktadır.
Gelecek yazımda vertex tabanlı modellemeyi işleyeceğim.
Kaynaklar:
(1): http://www-evasion.imag.fr/Membres/FrancoisFaure/doc/inventorMentor/sgi_html/ch08.html
Sorularınız için : [email protected]
Makale:
3D Grafik Programlama 2 : NURBS C++ ve C++.NET dili Özkan Eren
|