|
|
|
C#'ta Özyenilemeli Algoritmalar (Recursion) |
|
| Gönderiliyor lütfen bekleyin... |
|
|
Özyenilemeli algoritmalar
tüm dünyada bilgisayar bilimleriyle ilgili bölümlerde veri yapıları ve algoritmalar
derslerinde detaylı olarak incelenir. Bu bağlamda biz de makalemizde özyenilemeli
algoritmaları geliştirmeyi ve C# ile kodlamayı öğreneceğiz. Önce konunun teorik
temelleri üzerinde duracağız. Daha sonra daha iyi anlaşılabilmesi için konu
ile ilgili örnekler yapacağız. Makaleyi bitirmeden önce ise klasik döngüler
ve özyenilemeli algoritmaları karşılaştıracağız.
Bir alogirtma geliştirirken
genelde döngüleri ve karar mekanizmalarını metodların içinde kullanırız. Fakat
bazı durumlarda döngüler yerine özyenilemeli algoritmalar kullanmak daha kolay
ve anlaşılır olabilir. Özyenilemeli (recursive) metodların püf noktası bu
tür metodların bir şekilde tekrar tekrar kendilerini çağırmalarıdır.
Özyenilemeli algoritmalarda
problemin en basit hali için çözüm bulunur. Bu en basit duruma temel
durum (base case) denir. Eğer metod temel durum için çağırılırsa sonuç
dönderilir Daha karmaşık durumlar için metod, temel durumdan yararlanılarak,
problemi çözmeye çalışır yani kendini çağırır. Karmaşık durumlar için yapılan
her çağrı recursion step olarak adlandırılır.
İsterseniz konunun
kafanızda daha iyi canlanması için klasik faktoriyel örneğiyle devam edelim.
Sıfırdan büyük herhangi bir n tamsayısının faktoriyelinin formülü şudur:
n!
= n * (n-1) * (n-2) * .... * 3 . 2 . 1 |
Ayrıca 0! ve 1!'in
değerleri bir olarak tanımlanmıştır. Mesela 5!
= 4*3*2*1 = 120'dir.
Bir sayının, mesela n,
faktoriyelini özyenilemeli değilde döngü kullanarak bulmak istersek aşağıdakine
benzer bir kod kullanabiliriz:
int
faktoriyel = 1;
for( int i = n; i >= 1; i-- )
faktoriyel *= i;
|
Kod 1: Döngü ile
Faktoriyel hesabı
Eğer bu problemi özyenilemeli
algoritma yardımıyla çözmek istersek şu noktaya dikkat etmemiz gerekiyor:
Daha açık bir yazım
ile;
5! = 5 * 4 *
3 * 2 * 1
5! = 5 * (4 * 3
* 2 * 1)
5! = 5 * (4!)
|
Aşağıda şekilde 5!in özyenilemeli
bir algoritmada nasıl hesablanacağını görüyoruz. Şeklin solunda 5!'den 1!'le
kadar her özyenilemeli çağrıdaki neyin çağrılacağı sağda ise sonuca ulaşılana
kadar her çağrıda dönen değerler yeralıyor.
C# diliyle özyenilemeli
biçimde Faktoriyel hesabı yapan bir metodu aşağıdaki gibi yazabiliriz. Bu fonksiyona
int tipinde sayi isimli bir değişken geçiriyoruz. Eğer sayi
1'den küçük veya eşit ise, ki bu temel durumdur, fonksiyon 1 değerini
dönderiyor. Diğer durumlarda ise fonksiyonumuz
sayi * Faktoriyel(sayi-1)
değerini dönderiyor.
private
static long Faktoriyel(int sayi)
{
if( sayi <= 1 ) // Eğer
temel durumsa 1 dönder
return 1;
else //
Temel durum değilse n * (n -1)! bul.
return sayi * Faktoriyel(
sayi-1 );
}
|
Kod 2: Özyenileme
ile Faktoriyel hesabı
Sıra örneğimizi
bir Windows uygulaması olacak biçimde programlayalım. Bunun için öncelikle aşağıda
gördüğümüz Form'u tasarlayalım. Metin kutusuna txtSayi ve düğmeye
btnHesapla isimleri vermeyi unutmayalım.
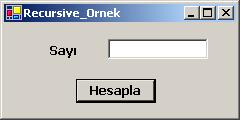
Formdaki btnHesapla
isimli düğmeye çift tıklayalım düğmenin Click olayına cevap veren metodu
yazalım.
private
void btnHesapla_Click(object sender, System.EventArgs e)
{
string sonucMetin="";
// metin kutusundan değeri
al ve int tipine çevir:
int sayi = Convert.ToInt32(txtSayi.Text);
for(int
i=1; i<= sayi; i++)
sonucMetin += i + "!=
\t" + Faktoriyel(i).ToString() + "\n";
MessageBox.Show(sonucMetin.ToString(),"Faktoriyel
Hesabı");
}
|
Kod 3: Örnek
programda btnHesapla_Click() metodu
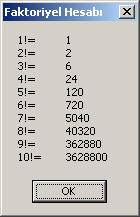
Yukarıdaki metod
içinde metin kutusuna girilen sayi değerine kadar olan tüm
faktoriyeller hesaplanıp ekrana mesaj kutusu içinde yazdırılıyor. Programımızı
çalıştırmadan önce programımıza Kod 2'de yeralan metodu da eklemeyi
unutmayınız. Örneğimizi 10 değeri için çalıştırırsak aşağıdaki sonucu elde ederiz:
Özyenilemeli Algoritma
Örneği: Fibonacci Serisi
Lise ve üniversitelerde
matematik derslerinde seriler konusunda gösterilen Fibanocci serilerini programlamak
için döngüler yerine özyenilemeli algoritma kullanmak daha kolay ve anlaşılır
oluyor. Bu serinin tanımı ise herhangi bir n sayısı için Fibonacci(n)'nin değeri
Fibonacci(n-1) ve Fibonacci(n-2)'nin şeklindedir. Tabiki Fibonacci(0) ve Fibonacci(1)'in
değeri 1 olarak alınıyor.
Bu serideki sayılar
doğada çok sayıda bulunur ve spiral şeklini oluştururlar. Ayrıca art arda gelen
iki Fibonacci değerinin oranı 1.68.. şeklindedir. Bu değer altın oran olarak
adlandırılır. Özellikle kart postallar, tablolar vb nesnelerin boy ve enlerinin
oranları da 1.68.. gibidir. Çünkü insan gözüne çok hoş görünürler. Neyse konumuza
devam edelim isterseniz...
Yukarıdaki tanımlardan
yola çıkarak Fibonacci serisini hesaplayan metod'ta iki temel durum olacaktır.
Bunlar Fibonacci(0) = 1 ve Fibonacci(1) = 1. Ayrıca diğer durumlar için dönen
değer, herhangi bir n için, Fibonacci(n-1) ve Fibonacci(n-2)'nin toplamıdır.
O zaman metodumuz aşağıdaki gibi olacaktır:
private
static long Fibonacci(int sayi)
{
if( sayi == 0 || sayi == 1) //
Eğer temel durumlardan biriyse 1 dönder
return 1;
else //
Temel durum değilse (n-1) + (n -2) bul.
return Fibonacci( sayi-1
) + Fibonacci( sayi-2 );
}
|
Kod 4: Özyenileme
ile Fibonacci serisi hesabı
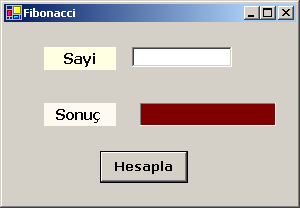
Fibonacci serisi
ile ilgili aşağıdaki küçük formu tasarlayalım. Sonra gerekli kodları yazıp örneğimizi
deneyelim. Formdaki metin kutusunun ismi yine txtSayi olsun.
Ayrıca Hesapla etiketine sahip düğmenin ismi btnHesapla olsun.
Son olarak arka planı koyu kırmızı olan etiketin ismi de label2 olacak.
Programı tamamlamak
için Hesapla düğmesinini tıklandığında gerekli işleri yapacak
kodu yazmaya geldi. Ayrıca programın kodunun içine Kod 4 yeralan
fonksiyonu da ekleyiniz.
private
void btnHesapla_Click(object sender, System.EventArgs e)
{
// Kullanıcını girdiği
değeri al ve int tipine çevir.
int sayi = Convert.ToInt32(txtSayi.Text);
// Fibonacci Hesabı
yapan fonksiyonu girilen sayi değeri ile çağır.
// Sonucu label2'ye yazdır.
label2.Text =Fibonacci(sayi).ToString();
}
|
Kod 5: Fibonacci
örneğinde btnHesapla_Click() metodu
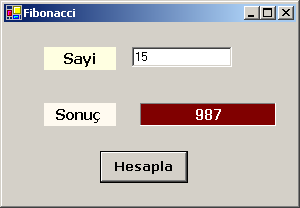
Programı test etmek için
Fibonacci(15) değerini bulmak istersek aşağıdaki sonucu elde ederiz.
Özyenilemeli Algoritma
Örneği: Fibonacci Serisi
Makalemizi bitirmeden
önce özyenilemeli algoritmalar ile döngülerden oluşan algoritmaların aralarındaki
farklara ve benzerlikte gözatmakta yarar olduğu kanısındayım. İki algoritma
türü de akış kontrol mekanizmlarını kullanır. Döngülerde for, while
ve do while yapıları kullanılırken özyenilemeli algoritmalarda
if, if/else ve switch yapıları yeralır. Aslında
hem döngüler de hem de özyenilemeli metodlarda itereasyonlar bulunur. Döngüler
doğaları gereği açık bir biçimde iteratiftirler. Fakat özyenilemeli algoritmalarda
iterasyon aynı metodun tekrar tekrar kendi içinden çağrılması ile gerçekleşir.
Döngülü ve özyenilemeli algoritmalarda göze çarpan diğer bir benzerlikte sonladırıcı
testlerin bulunmasıdır. Döngülerde sayacın(counter) belli bir değere ulaşıp
ulaşmadığı kontrol edilir ve gerekirse döngü sonlanır. Özyenilemeli algoritmalarda
o andaki durumun temel durum olup olmamasına göre işlemler devam edebilir veya
sonlanabilir. Son olarak hem döngülerle hem de özyenilemeli algoritmalar ile
bilgisayarı sonsuz döngüye(infinite loop) sokabiliriz. Birincisi döngünün sonlanacağı
sayaca ulaşmanın imkansız olmasından ikincisi ise temel duruma ulaşamamaktan
kaynaklanır.
Aslında özyenilemeli
algoritmaları kullanırsak hem daha yavaş hem de hafızada daha çok yer kaplayan
programlar yazmış oluruz. Fakat çoğu zaman aynı problemin çöümünü özyenilemeli
olarak bulmak daha kolaydır. Ya da döngülerle aynı sonuca varacak algoritmayı
düşünmek zor olur. Ayrıca özyenilemeli algoritmaları inceleyince anlamak ve
hata ayıklamak daha kolaydır. Bu durumda seçim programcıya kalmıştır. Yalnız
işlemcilerin giderek hızlanması, hafıza fiyatlarındaki düşüşü ve programın daha
kolay yönetilebilmesinin getirdiği avantajları göz önüne almanızı tavsiye ederim.
Bu makalede özyenilemeli
algoritmaları detayları ile inceledik. Konu ile ilgili sorularınızı rahatlıkla
sorabileceğinizi belirterek makalemize son verelim.
Makale:
C#'ta Özyenilemeli Algoritmalar (Recursion) C#, Visual C# ve .NET Ahmet Faruk Nacaroğlu
|
|
|
|
|
-
-
Eklenen Son 10
-
Bu Konuda Geçmiş 10
Bu Konuda Yazılmış Yazılmış 10 Makale Yükleniyor
Son Eklenen 10 Makale Yükleniyor
Bu Konuda Yazılmış Geçmiş Makaleler Yükleniyor
|
|
|